Как работают нейросети? Разбор

Нейросети, машинное обучение, искусственный интеллект. Звучит круто, но как это всё работает?

Объясню на простом примере. Представьте школьника, который пыхтит над контрольной по математике. И вот он подобрался к последнему уравнению, где нужно было вычислить несколько неизвестных (a, b и c) и посчитать ответ.

(a+b)*c=?

Он решает задачу и вдруг краем глаза замечает, что правильный ответ 10, а у него вообще не то — 120 тысяч. Что делать? По-хорошему, надо бы заново всё считать. Но времени мало. Поэтому он решает просто подогнать значения в уравнении, чтобы получился правильный ответ.

Он это делает и понимает, что значения a, b и с он посчитал неправильно еще в предыдущем уравнении. Поэтому там тоже надо всё быстро поправить. Он это делает и сдаёт работу.

Естественно, учительница палит, что он просто подогнал решение под правильный ответ и ставит ему двойку. И зря! Потому что, жульничество школьника на контрольной, можно считать прообразом метода машинного обучения, который позволил нейросетям совершить революцию в развитии компьютерного зрения, распознавания речи и искусственного интеллекта в целом. На разработку этого метода ушло целых 25 лет! И называется он алгоритмом обратного распространения ошибки.

Да-да, машинное обучение — это фактически подгонка уравнения под правильный ответ. Но давайте немного углубимся и поймем как это всё работает на самом деле, на примере простейшей нейросети.

Классические алгоритмы

Допустим, мы хотим научить компьютер распознавать рукописные цифры.

Как решить эту задачу? Отличник бы воспользовался классическими математическими методами.

Он бы написал программу, которая может определять специфические признаки, которые отличают одну цифру от другой. Допустим в 8-ке есть два кружочка, в 7-ке две длинные прямые линии и так далее. Вот только выявлять, что это за признаки и описывать их программе ему бы пришлось вручную. Короче надо было проделать кучу работы, и он бы всё равно обломался.

С такими задачами отлично справляются нейросети, потому как нейросеть может выявлять и находить эти специфические признаки самостоятельно. Как она это делает?

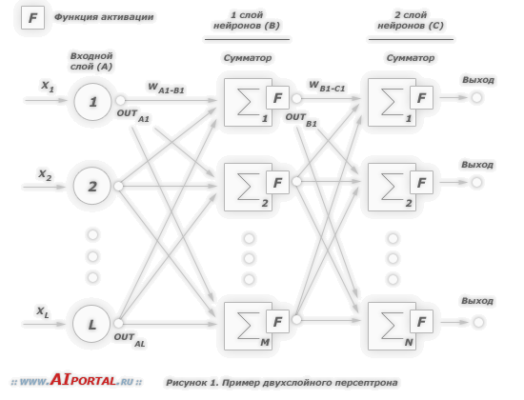
Для примера возьмём нейросеть с классической структурой, под названием многослойный перцептрон.

Структура нейросети

Нейросеть состоит из нейронов, а каждый нейрон — это ячейка, которая хранит в себе какой-то ограниченный диапазон значений. В нашем случае это будут значения от 0 до 1. На вход каждого нейрона поступает множество значений, а на выходе он отдаёт только одно. Наша нейросеть называется многослойной, потому, что нейроны в ней организованы в столбцы, а каждый столбец — это отдельный слой. Как видите тут целых четыре слоя.

Самый первый слой называется — входным. По сути, туда просто поступают входные данные.

Например, если мы хотим распознать картинку с цифрой размером 28 на 28 пикселей нам нужно, чтобы в первом слое нашей сети было 784 нейрона, по количеству пикселей в картинке.

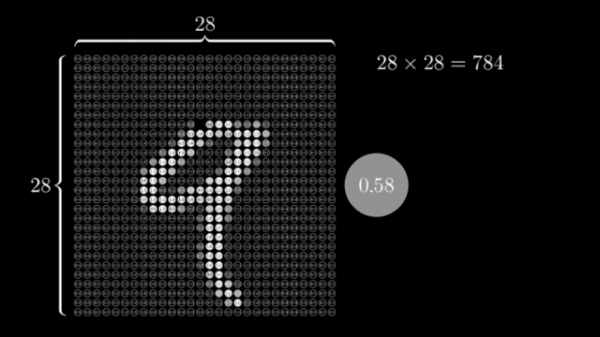
Так как нейросеть может хранить только значения от 0 до 1 закодируем яркость каждого пикселя в этом диапазоне значений.

Следующие два слоя называются скрытыми. Количество нейронов в скрытых слоях может быть каким угодно, это подбирается методом проб и ошибок. Именно эти слои отвечают за выявление специфических признаков.

Значения из входного слоя поступают в скрытые слои, там происходит специфическая математика, значения преобразуются и отправляются в последний слой, который называется выходным.

В том нейроне выходного слоя, в котором окажется самое высокое значение, и высчитывается ответ. Поскольку в нашей нейросети мы распознаем цифры, то в выходном слое у нас 10 нейронов, каждый из которых обозначает ответ от 0 до 9.

Веса и смещения

Структура примерно понятна, но какие данные передаются по слоям и что за специфическая математика там происходит?

Разберем на примере одного из нейронов второго слоя.

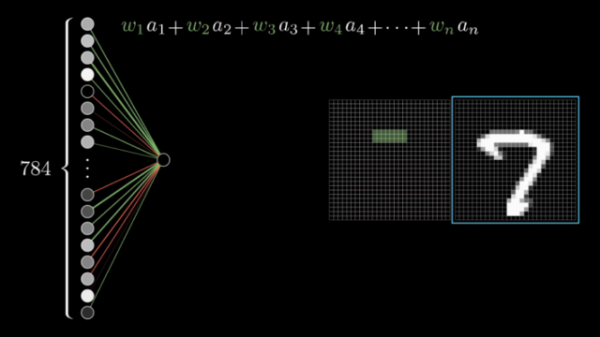
В этот нейрон, как и в другие нейроны скрытого слоя, поступает сумма всех значений нейронов входного слоя. Напомню, что задача нейронов второго слоя — находить какие-то признаки. Например, этот нейрон мог бы искать горизонтальную линию в верхней части цифры 7.

Если бы мы действовали в логике классического алгоритма, то мы бы могли присвоить разным областям разные коэффициенты. Например мы предполагаем, что в верхней части изображения должны быть яркие пиксели, например горизонтальная палочка у 7-ки. Для этой области мы можем задать повышенные коэффициенты, а для других областей — пониженные. Такие коэффициенты в нейросетях принято называть весами. В формулах обычно обозначаются буквой w.

Теперь смотрите: перемножая входные значения яркостей на веса мы понимаем, была в этой области палочка или нет. Если признак найден, то в нейрон будет записано большое число, а если признака не было — число будет маленьким.

Но для того, чтобы активировать нейрон, нам нужно подать туда достаточно высокое число, выше какого-то порогового значения. В противном случае, нейрон выпадет из игры и дальше ничего не передаст.

Как это делается?

Мы знаем, что нейрон может содержать значения от 0 до 1. Но входяшие данные могут иметь значение существенно больше: мало того, что мы суммируем все значения из первого слоя, так мы еще их перемножаем на веса. Поэтому полученное значение нам нужно нормировать, например, при помощи  функции типа сигмоиды или ReLU.

Но представьте, что на исходных картинках может быть шум, какие-то точки, черточки и прочее. Этот шум нужно как-то отсекать. Для этого в формулу вводится коэффициент смещения, по английски Bias, и он обозначается буквой b. Например, если Bias отрицательный — нейрон будет активироваться реже.

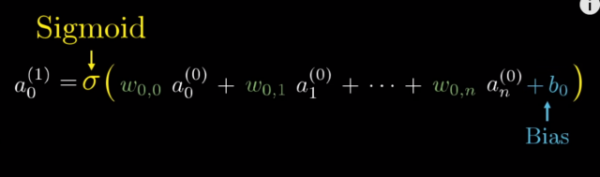
Вся эта функция, кстати называется функцией активации.

Все веса и смещения для каждого нейрона настраиваются отдельно. Но даже в небольшой нейросети типа нашей, весов и смещений более 13 тысяч. Поэтому вручную их настроить не получится. И как же нам задать правильные веса?

Обучение

А никак! Мы просто даем нейросети произвольные значения весов и смещений. И в итоге, естественно, мы получаем совершенно случайные ответы на выходе.

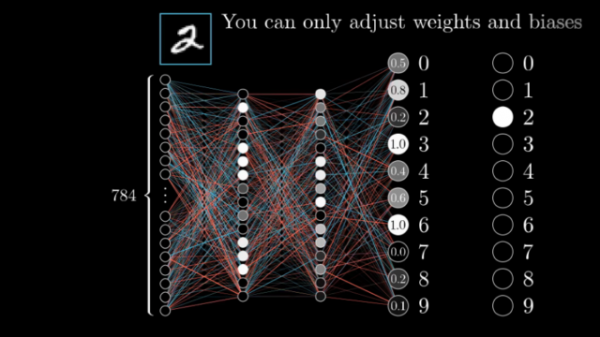
И вот тут мы можем вспомнить, что у нас, как и у двоечника в начале рассказа, есть преимущество. Мы знаем правильные ответы, а значит в каждом конкретном случае. мы можем указать нейросети насколько она ошиблась. И тут в бой вступает тот самый алгоритм обратного распространения ошибки! В чем его суть?

Допустим, мы загрузили в нейросеть цифру 2. если бы нейросеть работала идеально в выходном нейроне отвечающем за распознавание двойки было бы максимальное значение равное единице. А в остальный нейронах были бы нолики. Это значит что нейросеть на 100% уверена, что это двойка, а не что-то иное. Но мы получили другие значения.

Однако, поскольку мы знаем правильный ответ, мы можем вычесть из неправильных ответов правильные и подсчитать насколько нейросеть ошиблась в каждом случае. А дальше зная степень ошибки, мы можем отрегулировать веса и смещения для каждого нейрона пропорционально тому, насколько они способствовали общей ошибке.

Естественно, проделав такую операцию один раз мы не сможем добиться правильных значений на выходе. Но с каждой попыткой общая ошибка будет уменьшаться. И только после сотен тысяч циклов прямого распространения ошибки и обратного, нейросеть сможет сама подобрать оптимальные веса и смещения. Вот и всё! Так и работают нейросети и машинное обучение.

Другие структуры

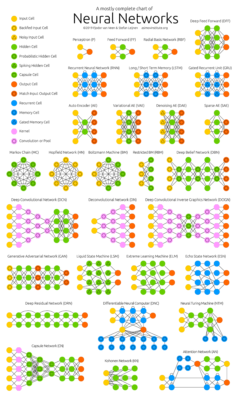
Мы с вами рассмотрели самый простой пример нейросети. Но существуют масса архитектур нейросетей:

• Нейросети с учителем
• Нейросети без учителя
• Нейронки, которые учат друг друга
• Нейронки, которые соревнуются между собой
• И даже нейросети, которые самостоятельно корректируют свою структуру в процессе обучения, наподобие того как это происходит в человеческом мозге.

Это целый мир чрезвычайно интересных знаний. И вскоре выйдет еще один материал про терминологию нейросетей и Искусственного Интеллекта.